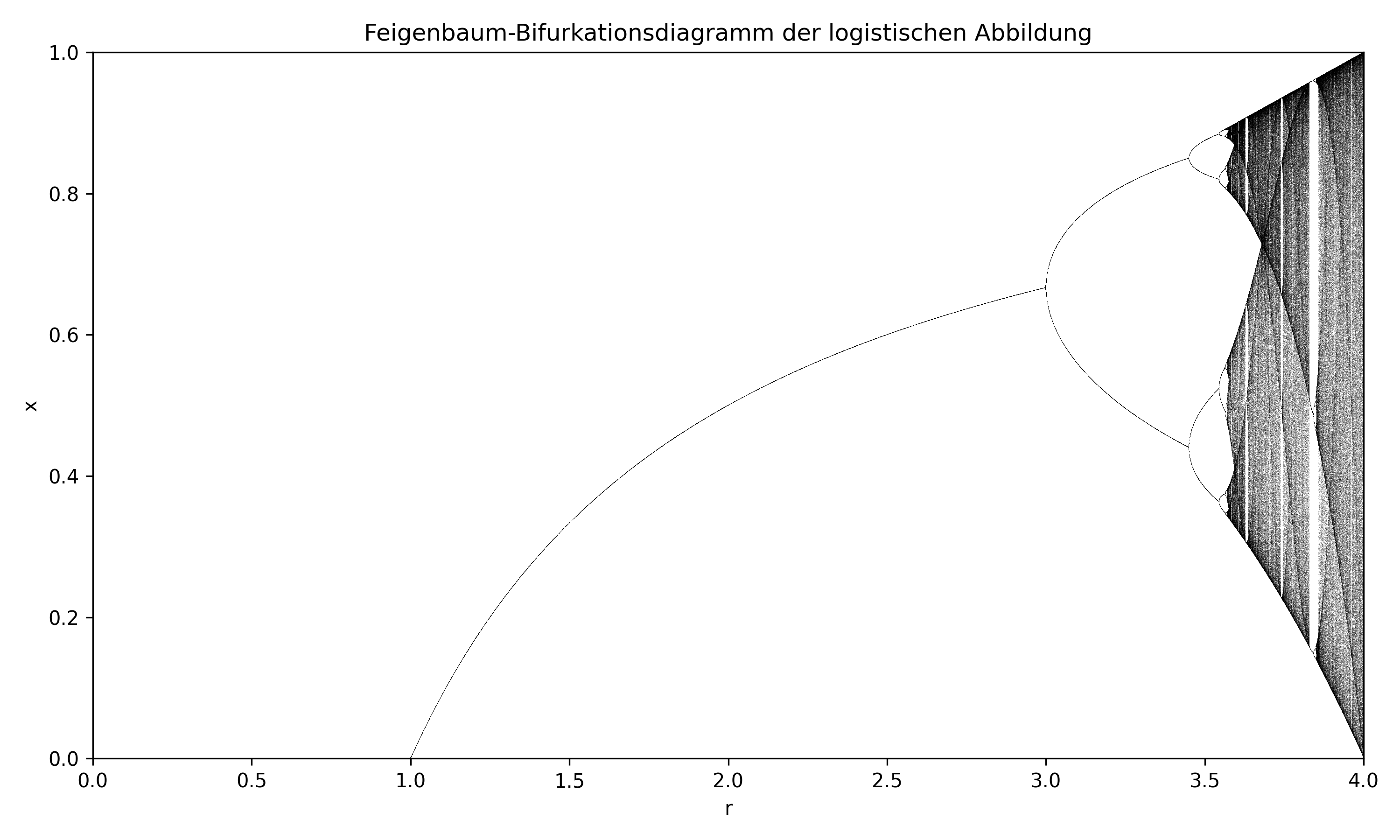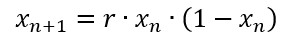
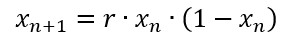

Man kann das per Hand rechnen:
r = 2 : Renditeparameter
n = 0:
x[0] = 0.1
n = 1:
x[1] = r * x[0] * (1 - x[0]) = 2 * 0.1 * (1 - 0.1) = 0.18
n = 2:
x[2] = r * x[1] * (1 - x[1]) = 2 * 0.18 * (1 - 0.18) = 0.2952
n = 1:
x[3] = r * x[2] * (1 - x[2]) = 2 * 0.2952 * (1 - 0.2952) = 3.2353
...
Oder per Software (Link zum Python Script) in der unteren Animation.
Links ist der Vermögensstand zwischen 0 und 1 (100%)
Unten ist die Periode n.
Mit Play startet man die Animation. Es werden verschiedene Werte für r vorgegeben. Man sieht die Dynamik der r-Werte:
Wenn man den Radiobutton auf Once stellt, kann man mit dem Slider einen r-Wert einstellen. In der unteren Tabelle gibt es Informationen zu den r-Werten. Ein Bild darunter ist das Feigenbaumdiagramm, in dem verschiedene r-Werte aufgetragen sind.
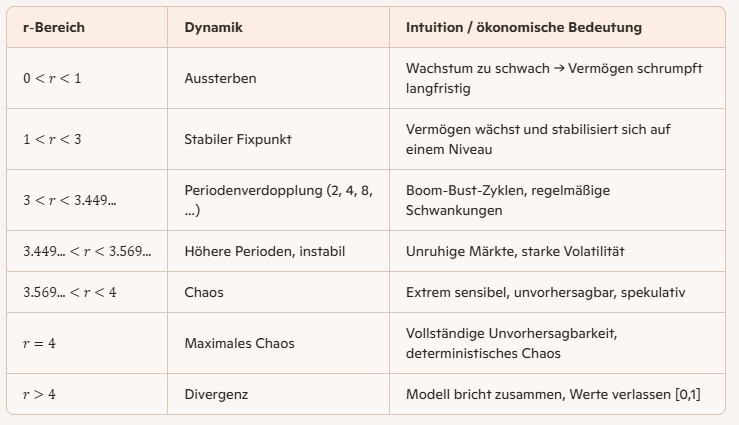
Im Feigenbaumdiagramm unten sind Beharrungswerte oder Chaos für bestimmte r-Werte. Das ist ein Fractal