Deutschland gehört zu den Ländern mit besonders hoher Vermögenskonzentration:
Die Vermögen können nicht unendlich wachsen, weil die Erde beschränkt ist. Ein Beispiel ist der Josephcent Wenn Josef bei Christie Geburt einen Cent angelgt hätte und das Geld verzinst wurde, dann wäre das Vermögen so groß, dass es soviel Wert wäre, wie die Erde aus Gold. Es ist ein Beispiel für exponentielles Wachstum.
Es gibt einen Startwert von 1.000.000 €. Dieser Startwert wird mit verschiedenen Steuersaätzen besteuert: 1%, 5% und 12%. In der Formel unten wird das neue Jahr (t+1) durch das alte Jahr (t) berechnet.
\[ x_{t+1} = (1 - s)\cdot x_{ t } \]Parameter der Folge:
\[ \begin{aligned} x_{t+1} &: \text{Kapital zum Zeitpunkt t} \\ x_{t} &: \text{Kapital zum Zeitpunkt t} \\ x_{0} &: \text{Anfangskapital} \\ s &: \text{Steuer als Dezimalzahl} \\ t &: \text{aktuelles Jahr} \end{aligned} \]Beim Faktor (1 - s) ist die 1 für das Summieren zuständig und das s ist eine negative Rückkopplung durch den Steuersatz.
Es gibt eine Schleife über n = 30 Jahre. Die ersten Jahre sind unten gezeigt:
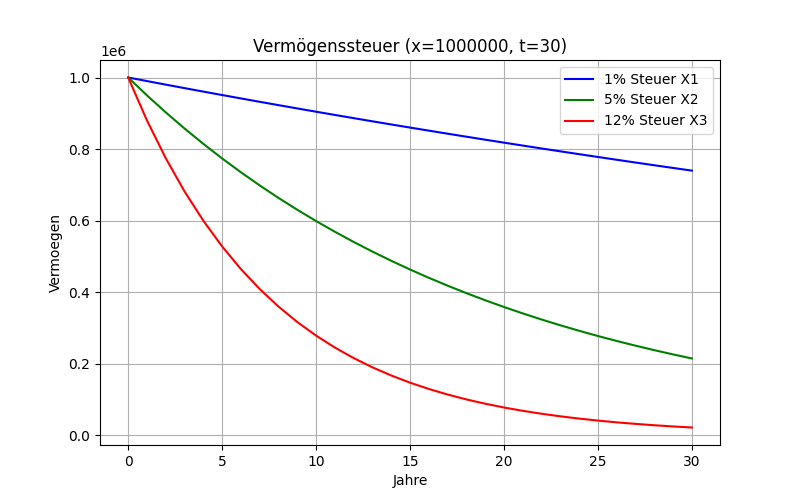
Man sieht das die Werte kleiner werden. In der Systemdynamik und Regelungstechnik nennt man ein solches System stabil. Der Nachteil ist, dass die Kurve gegen Null geht. Es ist wie ein Regler, der den Sollwert Null hat. Später sird ein Regler mit Sollwert vorgestellt.
Die Berechnungen kann man mit einem Python Skript machen. Der Plot ist in unterer Grafik dargestellt. Es gibt die Steuersaätze 1%, 5% und 12%
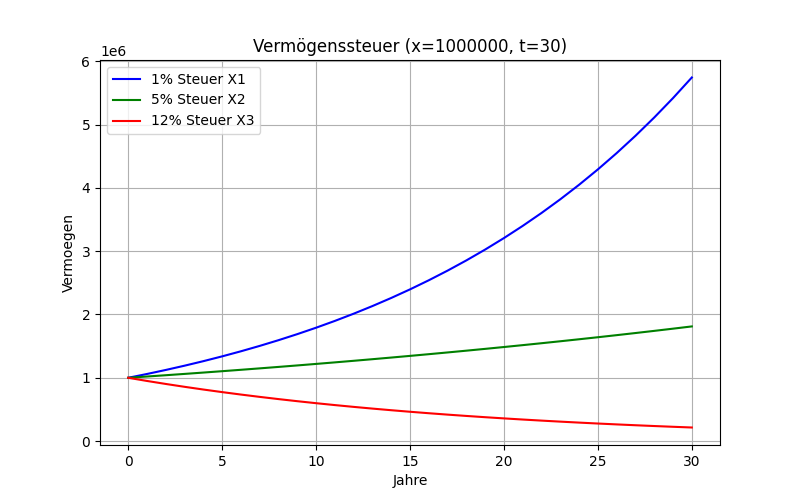
Es gibt einen Startwert von 1.000.000 €. Dieser Startwert wird mit verschiedenen Steuersaätzen besteuert: 1%, 5% und 12%. Jedoch gibt es auch 7% Zinsen für die Anlage des Vermögens. In der Formel unten wird das neue Jahr (t+1) durch das alte Jahr (t) berechnet.
\[ x_{t+1} = (1 - s + p)\cdot x_{ t } \]Parameter der Folge:
\[ \begin{aligned} x_{t} &: \text{Kapital zum Zeitpunkt t} \\ x_{0} &: \text{Anfangskapital} \\ s &: \text{Steuer als Dezimalzahl} \\ p &: \text{Zins als Dezimalzahl} \\ t &: \text{aktuelles Jahr} \end{aligned} \] Beim Faktor (1 - s + p) ist die 1 für das Summieren zuständig und das s ist eine negative Rückkopplung durch den Steuersatz. Es gibt eine positive Rückkopplung durch den Zins p.Es gibt eine Schleife über n = 30 Jahre. Die ersten Jahre sind unten gezeigt:
Man sieht, dass die Werte größer werden. (1 - s + p) = (1 - 0.01 + 0.07) = 1,07 > 1. Das System ist instabil.
s = 0.12: SteuersatzMan sieht, dass die Werte kleiner werden. (1 - s + p) = (1 - 0.12 + 0.07) = 0,95 < 1. Das System ist stabil.
Die Berechnungen kann man mit einem Python Skript machen. Der Plot ist in unterer Grafik dargestellt:

Bei 1 % Steuer wächst das Vermögen exponentiell. Bei 5% Steuer wächst das Vermögen nicht so schnell. Bei 12 % schrumpft das Vermögen. Es ist aber stabil.